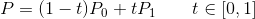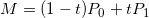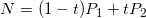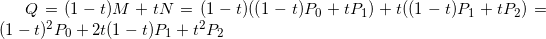挖一挖贝塞尔曲线那些事
一、前世今生
贝塞尔曲线的最初设计是服务于工业设计,尤其应用与汽车曲线设计。随着计算机画图的应用广泛,若想在计算机上画出平滑精准的曲线并不是一件容易的事,贝塞尔曲线解决了这样的问题,贝塞尔虚线通过起始点与结束点来确定曲线的首尾,通过若干个控制点来确定曲线的走向。由于其由法国工程师皮埃尔·贝塞尔广泛推广,因此这种曲线被命名为贝塞尔曲线。
二、数学基础
平面上的任意连续曲线可以通过伯恩斯坦多项式来进行逼近拟合,因此,当我们想在平面中画一条曲线的时候,如果可以模拟出此曲线的函数,则可以十分精准的控制计算机来描绘一系列曲线上的点来绘制曲线。贝塞尔曲线就是基于这样的数学基础。
首先,对于一条贝塞尔曲线,其3要素分别是:起始点,结束点和控制点。其中曲线的起点在起始点,终点在结束点,曲线并不穿过控制点,控制点来掌握曲线的走向,控制点个数可以不定。
1、一阶贝塞尔曲线
一阶贝塞尔曲线控制点的个数为0,只有起始点与结束点。其实一阶贝塞尔曲线就是一条从起始点到结束点的直线段。其公式如下:
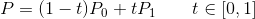
上面公式中,P为曲线上的点,P0为起始点,P1为结束点。(对于平面上的点,分别用上面公式计算x,y坐标即可)。由于其公式为线性公式,所有这种贝塞尔曲线也被称为一阶贝塞尔曲线。下图可以很好的描述当t从0到1变化时,线段的绘制过程:

2、二阶贝塞尔曲线
二阶贝塞尔曲线有一个控制点,假设起始点,控制点和结束点分别为P0、P1、P2。连接P0P1,P1P2,在区间0-1之间,在P0P1线段上取点M,在P1P2线段上取点N,使得P0M/P0P1=P1N/P1P2,找到线段MN上一点Q,同时使得MQ/QN=P0M/P0P1=P1N/P1P2,所有Q点的集合即为所求贝塞尔曲线。上面的描述有些抽象,使用数学推导就义一目了然了,公式推导如下:
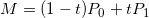
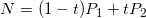
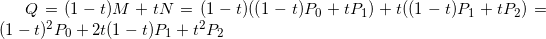
绘图过程如下:

3.高阶贝塞尔曲线
有了一阶与二阶的基础,高阶贝塞尔曲线也是通过相同的方式来推导,一个通用的递推公式如下:
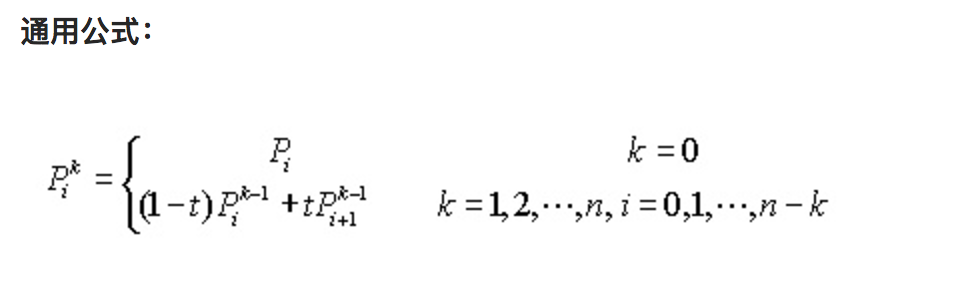
三阶和四阶的绘制过程演示如下:

三、iOS中的贝塞尔曲线的应用
虽然贝塞尔曲线在很多开发领域都十分容易实现,由于我对iOS开发比较熟,并且上面的曲线绘制示例也是我通过iOS程序实现的。这里就对在iOS中应用贝塞尔曲线进行简单的讨论,首先CoreGraphics核心图形框架中提供了CGPath可以直接创建贝塞尔曲线,系统支持的贝塞尔曲线函数有二阶与三阶。前面有博客专门讨论,这里就不再赘述,地址如下:
https://my.oschina.net/u/2340880/blog/757072。
这里主要列举UIKit框架中的UIBezierPath类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
+ (instancetype)bezierPath;
+ (instancetype)bezierPathWithRect:(CGRect)rect;
+ (instancetype)bezierPathWithOvalInRect:(CGRect)rect;
+ (instancetype)bezierPathWithRoundedRect:(CGRect)rect cornerRadius:(CGFloat)cornerRadius;
+ (instancetype)bezierPathWithRoundedRect:(CGRect)rect byRoundingCorners:(UIRectCorner)corners cornerRadii:(CGSize)cornerRadii;
+ (instancetype)bezierPathWithArcCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise;
+ (instancetype)bezierPathWithCGPath:(CGPathRef)CGPath;
@property(nonatomic) CGPathRef CGPath;
- (void)moveToPoint:(CGPoint)point;
- (void)addLineToPoint:(CGPoint)point;
- (void)addCurveToPoint:(CGPoint)endPoint controlPoint1:(CGPoint)controlPoint1 controlPoint2:(CGPoint)controlPoint2;
- (void)addQuadCurveToPoint:(CGPoint)endPoint controlPoint:(CGPoint)controlPoint;
- (void)addArcWithCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise;
- (void)closePath;
- (void)removeAllPoints;
- (void)appendPath:(UIBezierPath *)bezierPath;
- (UIBezierPath *)bezierPathByReversingPath;
- (void)applyTransform:(CGAffineTransform)transform;
@property(readonly,getter=isEmpty) BOOL empty;
@property(nonatomic,readonly) CGRect bounds;
@property(nonatomic,readonly) CGPoint currentPoint;
- (BOOL)containsPoint:(CGPoint)point;
@property(nonatomic) CGFloat lineWidth;
@property(nonatomic) CGLineCap lineCapStyle;
@property(nonatomic) CGLineJoin lineJoinStyle;
@property(nonatomic) CGFloat miterLimit;
@property(nonatomic) CGFloat flatness;
@property(nonatomic) BOOL usesEvenOddFillRule;
- (void)setLineDash:(nullable const CGFloat *)pattern count:(NSInteger)count phase:(CGFloat)phase;
- (void)getLineDash:(nullable CGFloat *)pattern count:(nullable NSInteger *)count phase:(nullable CGFloat *)phase;
- (void)fill;
- (void)stroke;
|
四、示例程序
下面是一个iOS平台的演示小Demo,使用它可以动态进行贝塞尔曲线的绘制并观察到辅助线与绘制过程,可以灵活的配置绘制的速度和控制点:

Github地址如下:
https://github.com/ZYHshao/Bezel。