从一些简单的例子看算法时间复杂度

在编程中，一段代码的执行效率实际上很难估算和预测，其主要受到如下几个方面的影响：

1.算法依据的数学基础。

2.编译器产生的代码质量和语言的执行效率。

3.问题的输入规模。

4.硬件的执行速度。

通常情况下，问题的输入规模和算法的数学基础是编码人员需要考虑的条件。时间复杂度是一个用来描述算法执行效率的重要标准。

在理解时间复杂度之前，你应该先了解什么叫做算法的时间频度，所谓时间频度即是一个算法解决问题所消耗的时间。但是一般情况下，一个算法解决问题消耗的时间通常与输入值有关，例如我们输入一个整数，找到比它小的所有正偶数，代码如下：

let n = 10;

for (var i = 0; i < n; i++) {
    if (i%2==0) {
        console.log(i);
    }
}

上面代码，当输入n为10时，循环会执行10次，如果时间频度t，则当输入n为20时，时间频度为2t。时间复杂度是用来描述随着问题规模n的变化时间频度t的变化规律。下面是一段更加数学风格的描述：

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

计算一个算法的时间复杂度时，我们可以将算法分解为逐条语句，计算每条语句的时间复杂度后再进行累加，如下代码的作用是对输入进行求累加：

let n = 10;  
let res = 0; //1
for (var i = n; i > 0; i--) { //1+(n+1)+(n+1)
    res = i+res;  //n
}
console.log(res);//1

当n输入为10时，时间频度为1+1+n+1+n+1+n+1 = 3n+5。设算法的时间复杂度函数为f(n),(3n+5)/f(n)当n趋于无穷大时，上式可以简化为3n/f(n)，取f(n)=n,上次结果为非零常数，因此此算法的时间复杂度为f(n)=n，记做O(n)。

当算法的执行时间频度和n无关时，算法的时间复杂度为O(1)，这是时间复杂度最小的函数，但是需要注意，时间复杂度小并不能说明算法执行耗费的时间短，比如一万行代码每行只执行一次的算法时间复杂度也为O(1)。

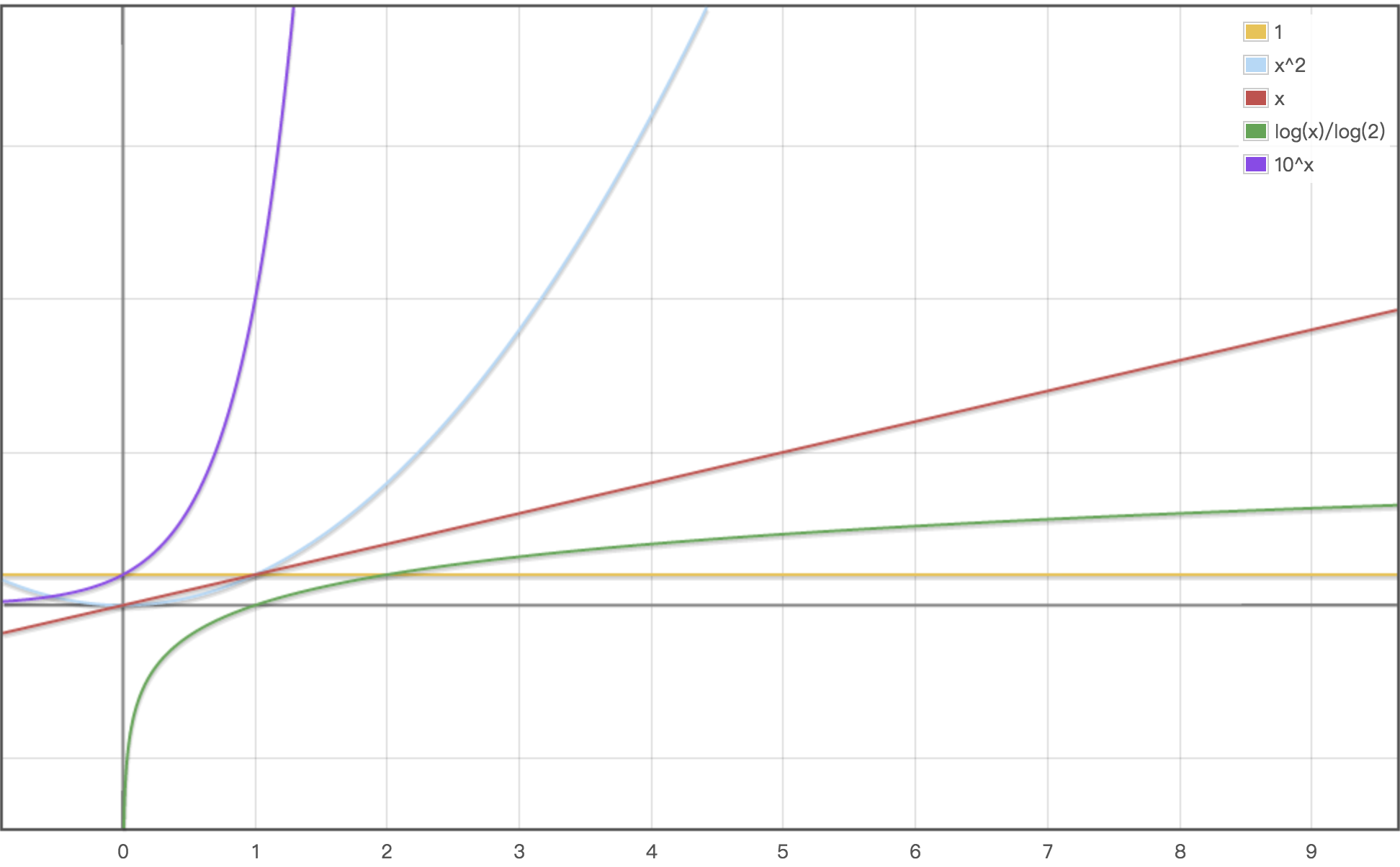
 常见的算法时间复杂度由小到大以此为：

Ο(1)＜Ο(log²_n_)＜Ο(n)＜Ο(nlog²_n_)＜Ο(_n_2)＜Ο(_n_3)＜…＜Ο(_2_n)＜Ο(n!)

其中O(log² n）是除了O(1)外时间复杂度最小的函数，例如如下代码：

let n = 10;  
var i = 1;

while(i<n){//2^t<n t<log2(n)  t为时间频度
    i = i * 2;
    tip++;
}

上面的时间频度为 1+1+log2(n)+log2(n)+log2(n)，去掉常数项后为3log2(n)，时间复杂度为O(log2(n))。如果将上面的代码在加一层循环，则时间复杂度会变为O(nlog3(n)):

let n = 10;  


for (var i = 0; i < n; i++) {// 1+n+1+n+1
    var j = 1;   //n
    while(j<n){//[3^t<n t<log3(n)]n  t为时间频度
        j = j*3;
    }
}

通过上面的示例，也很容易可以看出，循环层数的增多会剧烈的增加算法的时间复杂度，如果在递归函数中使用循环，则很容易产生时间复杂度为O(n!)的代码，从数学上看，这种代码随着输入复杂度的增加性能会急剧下降，在使用递归加循环时，还是要多多注意，示例代码如下：

function func(n) {  //n
    if (n<0) {
        return;
    }
    var i = 0;    //n
    for (; i < n; i++) { //n*(n-1)*(n-2)...*1
        console.log("tip");
    }
    func(--i);
}
func(10);

上面示例的JavaScript代码当传入n为150时的耗时已经和正常循环10000次的相同。